
Below we cover the the most frequently asked questions about the National Merit Scholarship Program. Please see our National Merit Semifinalist Cutoffs page for the latest information on actual and projected Selection Index cutoffs by state.
What is the National Merit Scholarship Program and how do you enter?
The NMSP is a program administered by the National Merit Scholarship Corporation in cooperation with the College Board to recognize high achieving high school seniors. Some recognition levels are based purely on junior PSAT/NMSQT scores, while other levels have additional qualifications (explained below). The NMSC gives out approximately $50 million in scholarships each year, and some colleges provide lowered—or even free—tuition to recognized students, multiplying the net impact of National Merit severalfold.
You must take the PSAT/NMSQT as a high school junior and either attend high school in the United States or U.S. Territories or be a U.S. student studying abroad. On your PSAT score report, you will see a section with your Selection Index and how you answered the questions about your entry eligibility. If there is an asterisk next to your Selection Index, it means that NMSC believes that you are ineligible.
What if I couldn’t take the PSAT?
Every year students miss the PSAT for legitimate reasons such as illness. To allow those students the opportunity to compete in National Merit, NMSC has a process known as alternate entry. Students must make a written request to NMSC for an alternate entry application form. The application itself must be signed off on by your principal or counselor and postmarked no later than April 1 after the missed PSAT/NMSQT.
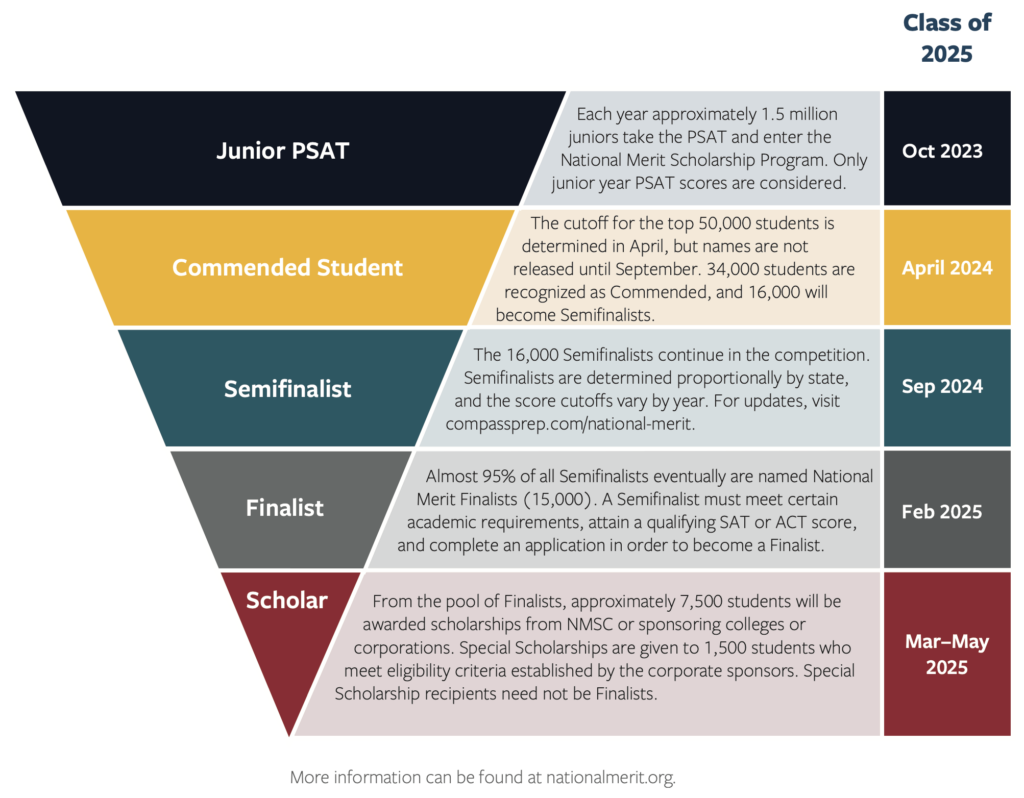
What is the Selection Index?
The Selection Index is a weighting of your PSAT component scores to determines the level of your recognition within the initial stages of the National Merit program.
How is the Selection Index calculated?
The Selection Index is double the sum of your Reading and Writing (RW) score, and Math score divided by 10. Alternatively, you can simply drop the last zero on your section scores, double the RW and add the Math. For example, a student with scores of 690 RW and 720 M would have a Selection Index of 69 x 2 + 72 = 210. You cannot directly calculate a Selection Index from a Total Score (320 – 1520). For students entering the competition with an SAT score through Alternate Entry, note that — when calculating a Selection Index — each SAT section is capped at 760. If, for example, you have a 700 RW and 800 Math, your Selection Index would be 70 x2 + 76 = 216.
Why is the Reading and Writing twice as important as the Math?
The emphasis on “verbal” skills has a long history with the NMSP. The digital PSAT no longer has separate Reading and Writing scores, but the RW score is still doubled.
I’ve already received my PSAT scores; how can I find out whether I will qualify for recognition?
Although you can use the Compass projections to estimate whether you are likely to qualify as a Commended Student or Semifinalist, there is no way of knowing your official status until high schools are notified by NMSC in early September of your senior year (sometimes schools hear by late August). Compass has published the cutoffs for the class of 2024 and estimates for the class of 2025. An historical archive dating back more than 15 years can be found here. The Commended cutoff for future classes becomes unofficially known in the April after the PSAT. Compass will report this score and how it may impact Semifinalist cutoffs on our regularly updated cutoffs post.
Will I qualify as a Semifinalist if I am in the 99th percentile for Selection Index according to my score report?
Although approximately 1% of test takers will become Semifinalists, there are a number of reasons why percentile scores are far too inaccurate to determine eligibility. Even the state percentiles that are now on the digital SAT report do not have enough information, because they are actually based on the prior 3 years of scores. Further, the percentile is rounded, and not accurate enough to determine cutoffs.
Why do some states have more Semifinalists and Finalists than other states?
Although Commended Scholars are honored based on a single, national cutoff, NMSC distributes Semifinalists proportionally to states (and District of Columbia and U.S. Territories) based on the number of graduating students in the state. For example, California sees approximately 2,100 Semifinalists each year—the most in the country. It gets 13% of Semifinalists because it produces approximately 13% of high school graduates. Mississippi, on the other hand, typically sees about 135 National Merit Semifinalists, because the state produces a bit more than 0.8% of U.S. graduates. The distribution is completely unrelated to the number of students taking the PSAT in the state.
Why are Semifinalist cutoffs so much higher in some states than in others?
Two things that have impact on cutoffs are participation rates and demographics. In some states, ACT is the dominant test and not as many students take the PSAT. This leaves some students out of the competition and will tend to produce lower cutoffs. Some states have large pockets of extremely qualified students and are particularly competitive. For example, Massachusetts and New Jersey have class of 2024 cutoffs of 222 and 223, respectively. At the other end of the spectrum, North Dakota, South Dakota, West Virginia, and Wyoming had NMSF cutoffs of 207 for the class of 2024. The minimum Semifinalist cutoff for a state is the national Commended level. If, for example, the Commended cutoff is at 210, no state can have a Semifinalist cutoff less than 210.
How are Semifinalists set for homeschoolers, boarding school students, or U.S. students studying abroad?
Homeschoolers are treated no differently than other students in a state. U.S. students studying abroad will have to meet the highest state cutoff in the country. For the class of 2024, that was 223. Boarding school cutoffs are the most complex to calculate. Instead of being set at the state level, they are determined regionally. A Northeast boarding school student, for example, must meet the highest cutoff of any state within the Northeast region. NMSC defines boarding schools as schools with predominantly out-of-state students. NMSC considers your state to be where you went to school when you took the PSAT, not your state of residency or the state of your new school.
Do I have to be a U.S. citizen to participate?
NMSC has made this part of the process easier to understand than it was in the past. Students at high school in the U.S. or in U.S. Territories are eligible. Period. Students studying abroad are eligible as long as they are U.S. citizens or lawful permanent residents of the U.S. (“green card”) or or have applied for permanent residence (the application for which has not been denied) and intend to become U.S. citizens at the earliest opportunity allowed by law.
Will NMSC notify me if I become a Semifinalist?
No. NMSC provides information only to schools until a student becomes a Finalist. Homeschoolers are the exception.
When will my school tell me?
NMSC mails information to schools in late August. Some schools let students know their status in early September. Many schools wait until NMSC officially releases student names to the press in the second week of September. Compass will track all of the latest news on our Semifinalists cutoff page.
Will being a Semifinalist help get me into my first-choice college?
While Semifinalist status is a nice award to list on your application, you should not expect it alone to have a significant impact on your admission chances at most colleges. The recognition tells college that you did well on the PSAT. Your SAT and ACT scores are far more important to colleges; your National Merit status does not add much new information. However, having a high number of enrolled Semifinalists is seen as a badge of honor at some colleges and will factor in their admission decisions. Some colleges have programs specifically to attract National Merit Finalists and offer large merit awards.
Do I need to take the SAT to become a Semifinalist?
No. Commended Student and Semifinalist recognition are based only on your Selection Index and your entry eligibility.
What happens after I am named a Semifinalist?
Semifinalists will receive login credentials for the Finalist application portal. You will need to provide background information and an essay. Your school will need to provide its recommendation and electronically submit your application in the second week of October,
What is the National Merit Finalist essay prompt?
NMSC may change the prompt in future years, but it has been the same for many years. It is broad enough that most students are able to use or slightly rework their Common App essay. For the class of 2024, the prompt was:
“To help the reviewers get to know you, describe an experience you have had, a person who has influenced you, or an obstacle you have overcome. Explain why this is meaningful to you. Use your own words and limit your response to the space provided.”
There is not a word limit specified, but the essay must fit within the provided space (approximately 3500 characters). Expect to keep your essay to 600 – 650 words.
Do I need to take the SAT or ACT to become a Finalist?
Among the requirements to proceed from Semifinalist to Finalist is that you receive a “confirming score.” This score helps validate that you can, on an official SAT or ACT test date, achieve a high score and confirm your testing skill.
Can a high ACT score be a confirming score?
Yes, the ACT can be used to confirm PSAT results.
How high of an SAT score do I need for a confirming score?
The confirming score is determined each year by NMSC and is calculated in the same way as the PSAT Selection Index. The confirming score is set nationally, so it does not matter what Semifinalist cutoff you met. The confirming SAT Selection Index (SSI) generally falls at or near the Commended cutoff.
The easiest calculation of the SSI is from your section scores. Drop a zero, double your RW, and add your Math score. For example, Student X might have a total score of 1450, with section scores of 720 RW and 730 M. Student X’s SSI would be 2(72) + 73 = 217. It’s possible for a student with a lower total score to have a higher SSI. Student Y has a total score of 1430, with section scores of 750 ERW and 690 M. Student Y’s SSI would be 2(75) + 69 = 219.
You cannot determine your SSI directly from your total score. One student scoring 1400 might have a high enough SSI, whereas another student with a 1400 might fall short. You must know your RW and Math scores.
How high of an ACT score do I need for a confirming score?
NMSC wants to have a level playing field, so it converts components of the ACT score into an SAT Selection Index. In order to do that, you need to use the official concordance tables published by ACT/College Board. There is no SAT Science, so NMSC does not look at ACT Science. So discard that score.
Step 1: Add your ACT English and ACT Reading scores
Step 2: Use the ACT E+R to SAT RW concordance table to find the concordant SAT RW score based on the sum in step 1. Be sure that you are going in the correct direction when using the concordance tables. ACT E+R to SAT RW is not always the same as SAT RW to ACT E+R.
Step 3: Use the ACT M to SAT M table to find the concordant SAT M score based on your ACT Math score.
Step 4: Calculate your SAT SI: drop the last zeros (i.e. divide by 10), double your RW, and add your Math score. You want this number to be at least as high as your class year’s Commended Student score.
Example:
A student has ACT scores of 32E, 34M, 33R, and 31S. Science is not used. The sum of E and R is 65. In the concordance tables, this is equivalent to a 700 RW. The 34 Math is concordant to a 760. This student’s SAT Selection Index is 70×2 + 76 = 216.
When do I have to take the SAT or ACT for the score to be ‘confirmed’?
You can use any SAT or ACT score from the fall of your sophomore year to December of your senior year. This means that you could have received an SAT confirming score even before taking the PSAT/NMSQT. NMSC recommends that you not wait until the December test date.
How do I submit scores to NMSC?
NMSC does not automatically know your SAT and ACT scores. You must submit them just as you would to a college. The College Board code for NMSC is 0085. The ACT code is 7984. Please verify these codes before submitting. Since NMSC will use your highest scores, there is no penalty for choosing them as one of your free score recipients when you register for the SAT or ACT.
Can I superscore SAT or ACT dates in order to reach the confirming score cutoff?
No. NMSC will use your highest scores, but will not superscore across test dates.
If I have achieved a confirming score, is there any reason to shoot for a higher score?
The requirement for a confirming score is simply true or false when applying to become a Finalist. However, your test scores are used to evaluate you during the scholarship phase of the competition. Depending on your goals, you may want to optimize your score.
Can sophomores qualify for National Merit recognition?
No. Even if your scores are high enough, you will not be eligible for National Merit as a sophomore unless you will be graduating a year early. In that case, you should contact NMSC or your principal about next steps as NMSC has no way of automatically knowing your eligibility.
Is it hard for a Semifinalist to become a Finalist?
Of the 16,000 Semifinalists, 15,000 become Finalists. You must go through an application process to proceed to Finalist level and then to compete for National Merit Scholarships. As part of the application, you must meet citizenship requirements, have a satisfactory academic record, achieve a confirming score on the SAT or ACT (and submit the scores to NMSC!), write an essay, and receive a recommendation from your principal. More information can be found in the PSAT/NMSQT Student Guide. In the Semifinalist letter from your school (it will NOT come from NMSC unless you are homeschooled), NMSC will provide details about how to begin the process online.
When will I find out if I am a Finalist?
You will be notified in February of senior year.
Do all Finalists receive scholarships? What is a National Merit Scholar?
Only about half of Finalists become National Merit Scholars and receive a National Merit Scholarship. There are three types of scholarships for Finalists, each with its own criteria. A student can only receive one type of scholarship. Approximately 4,000 Finalists receive scholarships from sponsoring colleges with renewable stipends of $500–$2,500 per year. Students must be accepted by a sponsoring institution and list the college as first choice in order to receive a college-sponsored award. These awards are not transferable to another college. Corporations sponsor approximately 1,000 awards for Finalists each year with a minimum one-time value of $2,500 or $1,000 renewable. Most of these awards are to Finalists who are the children of employees. Approximately 2,500 students receive awards of $2,500 directly from National Merit. These awards are highly competitive and are allocated proportionally by state. A list of sponsoring colleges and corporations can be found in the PSAT/NMSQT Student Guide.
I’ve heard about colleges that provide full-ride awards. Why are college-sponsored awards only listed as $500–$2,500 per year?
Colleges can also choose to provide additional awards to National Merit Finalists. These are not technically National Merit Scholarships, but they can be the most important awards for many students. Which colleges offer these awards and how much they offer can change from year to year. In recent years, Florida has had a generous scholarship program for National Merit Finalists, and schools such as UT-Dallas and Texas A&M also provide substantial awards. Compass does not maintain a database of scholarships. The National Merit forum at collegeconfidential.com is a useful resource.
Are scholarships available to Commended Students and Semifinalists?
Technically, these students cannot be National Merit Scholars, but approximately 1,100 of them will receive Special Scholarships from sponsoring corporations. As with other corporate-sponsored awards, these are predominantly for the children of employees, although companies can also identify students in a particular region or field of study.
When will I find out if I receive a scholarship?
You will be notified of scholarship status sometime between March and June of your senior year. In order to receive a college-sponsored scholarship, you must note the college as your first choice on the National Merit application. It can be to your advantage not to immediately choose a first-choice college—you can leave it as “Undecided.” You do not want to miss out on a large scholarship because you have listed the wrong college. There is no reason to list a college that does not provide National Merit Scholarships. List your first-choice among college that do provide scholarships. You can update your choice via the Online Scholarship Application portal.


My son was selected as Semi-Finalist. He fits the criteria for the other boxes ….application asked for recommendation, but not specifically through Principal – he obtained it through 2-time teacher and 4-yr coach (explanation indicated Principal). I have question on #1 choice. He did put #1 choice school down as it offers cost of attendance benefit and he’s leaning that way anyway. His other considered school offers essentially nothing for NMF so it seems to make sense. However, what if he doesn’t get accepted into that school? I would think he would get in given his other credentials, but with the “wholistic” application, you just never know and I never want to “assume”. Admission acceptance doesn’t come out until mid March. Is this one of the reasons to go “undecided”? If he doesn’t get accepted, can he change to another school at that point or is that when it’s too late? Isn’t he able to change his #1 school until May?
Julie,
On such an important question, I would recommend a call to NMSC. I can tell you that the choice won’t matter until the first round of names are sent to first-choice colleges on March 1. This is a match-making process, and colleges have to make an offer to a student. I may be wrong, but it doesn’t seem like a college would make an offer without intending to accept a student. I think this avoids the worst-case-scenario in your case. Your son could leave himself as “Undecided” and change this only after acceptance. The risk there is if a college limits the number of awards it provides. A school with a cost of attendance benefit usually has a liaison to deal with NM questions. Based on the situation you’ve described, I would have your son list the college providing sponsorship. You’d then have time to do further research with the school and with NMSC to make sure that things go according to plan. “Undecided” is more important when there are multiple scholarship-providing schools that a student is still considering. Again, when it comes to such an important award, don’t trust a guy on the internet!
“Guy on the internet” – LOL….I’ll reach out to NMSC. Thanks!
Hi Mr. Sawyer;
curious about the PSAT test taken on October 24 2018 alternative date.
Like others have mentioned, just missing one or two questions could have knocked someone out from being a NMSF.
My question is this: how many took the test on the 24th of October in 2018; and how many of them are NMSFs? is there any way to know that? Is it a similar ratio as to those taking it on the original date?
It was very disappointing to be knocked out of contention when my kid had to take it on October 24 because of a school disruption earlier in October. I’d be interested in your thoughts about this all. THANKS!
Jen,
About 10% of test takers took the alternate date — somewhere around 150-170K. Neither College Board nor NMSC release any score or Semifinalist data by test date. The assumption is that the test scaling equates the two exams. The Oct 24, 2018 exam had easier questions, so it had a harsher scale. It was way out of the norm, though, and I suspect that it did a poor job for National Merit purposes. It’s not quite as easy as saying it produced a lower number of Semifinalists — it would, however, have done it in a more arbitrary fashion. I’m sorry that it did not work out in your son’s favor.
Hi, Mr. Sawyer!
Thank you for writing this detailed article. I had many questions about my first PSAT test, and I am so grateful I could find a dependable source like you. I am a sophomore student in California, and I recently took the PSAT/NMSQT. Here are my scores:
– 710 for the Evidence-Based Reading and Writing Score
– 690 for the Math Score
– 1400 for the PSAT/NMSQT Total Score
– 211 for the NMSC Selection Index Score
Will I be able to be recognized as Commended Student, or are scores for the PSAT/NMSQT not eligible for anything?
Thank you for your time!
JK,
As a sophomore, you are not yet eligible to compete in the National Merit Scholarship Program. You have an excellent score, and Semifinalist status is within range for next year. Expect to need around a 222 next year (Commended is likely to fall in the 211-213 range). But you still have a lot of time before needing to worry about that. Congratulations on a great job.
Hi Art,
Will you post when the Finalist letters are mailed? Thanks.
Katie,
Since Finalist letters go directly to students, I need to hear about mailings from other commenters. I will publish as soon as I do (and please update me if you have heard).
Hello,
My son, who is a Junior scored 36 in his ACT, but he did not take ACT Writing section. He took ACT last year(10th grade) with Writing. He scored 35 composite score and got 8 on his writing part.He got 1490 in his PSAT and got 224 SSI(Minnesota)
I have couple of questions….
1)when we apply for college admission, which ACT score would be the best option?
2) Sure, he will be NMSF. What score would be good for his NMF application?
Please Advise.
Thanks Mr.Art.
PRG,
1) The Writing test has been essentially given up on by virtually all colleges (the University of California should formally announce soon, we hope). There will be no reason to report his 35 unless he is applying to West Point (I hope that they will finally drop Writing, as well).
2) NMSC does not consider Writing or Science. So likely his 36 unless the 35 is better for E/R/M.
Dear Mr.Art,
Thanks a lot for your information and valuable advise as always. His ACT score is 36(Math-36, English 36, Reading 36 and Science 35). So, we will use his ACT score 36 for his NMF application when time comes.
Thanks again for all your help and advise Mr.Art.
Hi Art,
I work for a gifted high school, I am looking for data that shows students ACT scores and becoming a finalist. Do you know where I can find this? Thank you!
B.Roach
Brittany.
If you mean the ACT scores needed as confirming scores, I cover the convoluted conversion to a Selection Index above. Since the confirming score is an all-or-nothing cutoff, there is just that conversion. NMSC doesn’t publish the confirming score, but it is usually the same as — or close to — the Commended level. Let me know if I misunderstood the question!
Art,
My son received a National Merit Scholarship from the University he will be attending. He was notified of being a Finalist and we are trying to clarify if he moved to the next level of becoming a National Merit Scholar. In his scholarship letter from NMSC, they referred to him as a “Merit Scholar designee”. Does that mean he is a National Merit Scholar or is that the term used for National Merit Finalists too? Thank you for all the information you provide.
Michelle,
Congratulations to your son. It’s curious wording that NMSC uses, but your son is a National Merit Scholar. Perhaps they choose to use “designee” because a student could always switch colleges and lose out on the scholarship. No, it is not a term used for all Finalists.
Hello Art,
I have a follow up question on NMSC – my son was awarded the scholarship and had committed to a particular college by the deadline they specified. However, he just got off the waitlist and has decided to go there instead. What is the method to get the scholarship money to the new school, since NMS website has closed the option to select the school where funds are to be sent. Have you had students in such a situation?
Bobby,
Hopefully you’ve contacted NMSC by this point. My guess is that he will not be able to transfer the award if it is school sponsored. If it is a corporate-sponsored scholarship, then NMSC should be able to handle it. Those awards follow the student. Let me know what you find out.
Hello, Mr. Sawyer,
Good evening. My son’s high school has not try notified him of the commended status. As I understand, they would usually do this before or at least by the second week of September? His index is 216 and NMSF in our state is 217, while commended is 209. Could you please tell us how the students are notified if their school chooses not to? My son did get the letter stating he was selected for the College Board Recognition Program, but of course, that is not the same. The school has not given him the certificate for that either. Is this normal? Thank you.
Kelly,
NMSC doesn’t send out Commended information to schools until the Semifinalist information is released (September 9 this year). Most schools should have received the packets by now. You can call NMSC, and they should be able to confirm your son’s status. He clearly scored high enough. I don’t know the policy on the CB Recognition Program, as they have changed it markedly. I was not aware of a certificate from the school.
Hello.
I hate to even ask this question because I’m very proud of my son’s recognition as commended for the 2019 NMSQT. His composite score of 219 would have him qualify as a semifinalist in 41 states; we live in Virginia where the cut score is 221. However, we do not live in Northern Virginia, Tidewater, or Charlottesville where the school systems are so very different from Southern Virginia where we live. Has anyone ever appealed the score based on diversity of the state? It seems to me that the College Board recognizes the disadvantage rural students inherently have since they recently created a National Rural and Small Town Recognition Program. (I only know this because he earned this recognition as well). What are your thoughts? It’s an ethical dilemma for me, yet I feel the need to advocate for my son (and one other student who was also commended). The school has only had one other commended student years ago. It’s a rarity in our area. Thank you for any advice you can share.
Kimberly,
I think a mixture of pride and indignation is merited. I had a lengthy discussion last year with a mother in an almost identical situation (her son was in southwestern VA). We see the same problems in other states, too, where the concentration of resources in metropolitan areas results in an extreme concentration of Semifinalists. Unfortunately, I’ve never heard of a successful challenge. National Merit is certainly aware of the situation and has chosen to ignore it for decades. College Board runs its recognition program separately from NMSC, which as full control over National Merit. Your battle is with NMSC, and you have nothing to lose in letting your voice be heard.
Hello Art — My child did SAT in December 2020 and has not been able to take the PSAT yet. Could you please help calculate the Selection Index based on the following scores:
39 Reading, 38 Writing and Language, 39.5 Math. Thank you so much!
SD,
When calculation a Selection Index the scores are capped at 38, since the highest achievable on the PSAT. That means your student received a perfect 228 SI: (2)(38+38+38). Congratulations! Be sure to complete the Alternate Entry application and send a score report to NMSC.
Hi Art,
I took the December SAT and got a 1540(740 RW and 800 Math). I wanted to enter the alternate entry process and I didn’t know if my score would be high enough. I live in New Jersey and it’s a really competitive state, so would I make the cutoff?
Billy,
Your Selection Index is 74×2 + 76 [Math is capped] = 224. That should be high enough. The only cost to enter the program is sending a score report to NMSC, so I strongly encourage you to complete the online application.
Hi Mr. Sawyer,
I am using the alternate entry method to attempt to qualify for the NMS. My SAT score converts to a 221 index (last year’s cutoff for my state, MD), according to the people I spoke to at the NMS corporation. If the cutoff stays the same, I will qualify. The cutoff is also on a downward trend for my state. Anyway, how do you think cutoffs will change given the pandemic and the reduced testing? Will the corporation be more lenient?
Thanks,
Nicolas
Nicolas,
I would not say that Maryland is trending downward. Its cutoff has tracked the fluctuations that we see from minor inconsistencies in the scale from year-to-year (compare how it aligns to California). Last year’s PSAT had a poorly scaled exam on the primary PSAT date, so cutoffs were low across the board. I’d say that the more natural level for Maryland is 222-223. HOWEVER, pandemic. The difficulty in testing this year will lead to downward pressure. It’s not that NMSC will be more lenient, it’s that fewer students will have taken the PSAT (see your own case as evidence). I think there is an excellent chance that 221 will qualify this year, but it’s impossible to say with certainty. The good news is that you already have a confirming score, so you are ready no matter what happens.
Hi Art,
Just from my curiosity. I’ve seen the posted images of the letters sent to national merit finalists with their first-choice college. Does it mean that the finalist has been already accepted to the college?
Thanks, John
Hoyoung,
I’m not sure that I know what letters you are referring to. Anything from NMSC, as far as I know, would only be confirming a student’s selection, since the matching process does not begin until March 1.
Hi Art,
My daughter is a National Merit semifinalist (2022). She qualified using her SAT score. Her selection index score was 226, the cutoff for our state is 219. For the confirming score, she is planning on submitting her ACT scores. But we recall that NMSC capped scores in computing the selection score. Are confirming scores converted from the ACT capped also?
Her scores are ACT English + Reading = 71, and ACT Math = 32. Using concordance tables we get 770 for SAT ERW and 720 for SAT Math. If NMSC caps her ERW score, could she end up with a nonqualifying score? Without a cap, her confirming score from the ACT should be 226. Is there a cap on computing confirming scores? Are we correct to think that there is no cap when confirming?
Thank you!
D.
Denise,
The confirming score is a national cutoff and is not the same as the state cutoff. In fact, it is typically set at the Commended level. Her ACT score easily clears the hurdle — with or without caps. I believe the Finalist portal has information on the conversion process. Sorry for the late reply!
Hi Art,
I am a junior and took SAT in Aug 2021 and scored 1550 (770 RW and 780 Math). Can I use my SAT score for alternate entry process for class of 2023? I also took PSAT in Oct 2021 but not sure I will score high enough.
Thanks
Ashely
Ashley,
A student with a PSAT score is not eligible for Alternate Entry. Great job on the SAT!
Hi Art,
A fire alarm went off during the administration of my daughter’s PSAT on Oct. 26. Does this qualify her for Alternate Entry, even though the students did complete the test after they returned to the building? You wrote here that a student with a PSAT score is not eligible for AE – but do you know if the NMSC makes exceptions to that rule for unusual circumstances like this that create unfavorable testing conditions? Is the NMSC told that the test had a nonstandard administration? And if they are told, is that a basis for AE?
Thanks for all that you do!
Katie
Katie,
It is possible to remove a PSAT score from consideration under certain circumstances. I believe the deadline to do so is rapidly approaching, so I encourage you to contact National Merit Scholarship Corp. It’s a no-going-back process, so your daughter would need to accept that her PSAT score will be ignored — even if she aced it. In addition to applying to have her PSAT invalidated for the purpose of National Merit, she will need to apply for Alternate Entry.
Hi Art, if a sophomore takes the PSAT and qualifies as a semi-finalist at that time, does he have to wait for his senior year to take the SAT if he is not going to be graduating early in order to qualify for the scholarship? Thank you.
Carole,
Short answer: No.
Long answer: Normally sophomores are ineligible for National Merit. The exception is when students are completing high school in 3 years. In that case, a student can participate in their last or next-to-last year (sophomore/junior/senior designations get confusing when a student is graduating early). The confirming SAT score can be earned any time between August two years prior to Semifinalist status through December post Semifinalist status. For example, a Semifinalist named in September 2021 needs a confirming SAT or ACT score between August 2019 and December 2021.
Dear Art:
In response to the FAQ: “Will I qualify as a Semifinalist if I am in the 99th percentile for Selection Index according to my score report?”, the FAQ above says: “Although approximately 1% of test takers will become Semifinalists, there are a number of reasons why percentile scores are far too inaccurate to determine eligibility, especially since cut-offs vary dramatically from state to state. The Compass projections are better estimates, but they are still just estimates.”
Could you give a more complete answer? Why are “percentile scores far too inaccurate to determine eligibility”? I understand that the cut-off to be a semi-fianlist varies by state. In particular, DD in Fall 2021 took the PSAT, had a composite percentile of 99, and a selection score of 207 for KS, were the selection score for semi-finalists is projected to be much higher (213 at the lowest). Kansas seems to be a middle-of-the-road state in terms of qualifying selection scores (unlike New York or DC, for example). Furthermore, the projected Commended Student selection score is 208, so even though DD is in the 99th percentile, her selection score is likely too low to be have the Commended recognition (let along be a semi-finalist, which is allocated to the top 1% in each state).
I know it will not change anything, but I would like to understand. Is the composite percentile based on some sort of extrapolated projection to all juniors in high school (and not just PSTA test-takers)? Something else?
Mark,
This is something of a hobby horse with me, so pardon the length.
There are a number of reasons why percentiles are unhelpful at best and misleading at worst for National Merit.
1. You are correct in your instinct that the first problem students and parents run into is that College Board prominently lists the Nationally Representative Sample Percentile, which is a make-believe number based on every student in the country taking the PSAT. The more relevant number is found deeper in the online report and is the User Percentile. This is based on students who took the PSAT.
2. But we are not out of the woods yet. The User Percentile is not based on CURRENT test takers. It is based on the performance of students who took the test in 2018, 2019, and 2020. So it tells us nothing about performance on the Oct 2021 exam. Given how the Commended cutoff can bounce around, that proves a problem.
3. It gets worse. The percentiles are provided for Total Scores, not the Selection Index. Total Scores do not convert directly into the Selection Index. For example, a 1400 Total Score could range from a Selection Index of 204 (640 ERW / 760 M) to a Selection Index of 216 (760 ERW / 640 M). That’s a huge swing when you are talking about National Merit eligibility.
4. There’s more. Percentiles are provided as integers. If we are trying to determine something precise like the top 16,000 scores, that matters. A 99th percentile score can represent anything from 98.51% to 99.49% (at 99.5%, 99+ takes over). So depending on where the 99th percentiles fall, there can be essentially a 1% difference. That’s going to make the numbers close to useless. [If everything else were accurate, we could at least interpolate between percentiles to estimate where the numbers likely fall. The distribution is not that of a normal curve, but it’s still a relatively stable curve.]
5. Not done yet. It’s easy to make a mistake in interpreting the percentiles. Let’s say the percentiles were reported with precision and a student’s percentile rank is 99.0%. It’s tempting to think that the student is in the top 1% of test takers (ignoring, for a moment, that it’s the top 1% of students over 3 previous classes). College Board reports percentiles based on students scoring AT OR BELOW a given score (an alternate form of calculating percentiles — one that College Board used to use — is the percent of students scoring BELOW a given score). This means that our 99.0% student has 1% of all students ABOVE her score. We need to look at the score below hers to determine where she is in the pecking order. If the score below hers is 98.4%, then 0.6% of students got her exact score. That means that she is in the top 1.6% of students. You can imagine how #4 and #5 intertwine to make exact estimates impossible.
6. Finally — although this could have been firstly — national ranks do little to help us determine state ranks (as you pointed out). A top 1% national scorer (again, pretending that we can really know this exactly for Selection Indexes, which we don’t) won’t qualify in New Jersey and will qualify in West Virginia. Accurate and current percentiles would help us with the Commended level, but the percentiles are neither. The number of students scoring in the 1400-1520 range is about the best we can do in determining performance on the Oct 2021 exam. I know of no other measurement for the current test.
So percentiles are not based on the students who took the test, are not based on the measure we actually care about, are imprecise, and are not at the state level. Prior cutoffs — although not based on the current class either — at least give us measures on the scale we care about, are at the state level, and have more granularity than a 3-year blend of percentiles.
Good luck to your daughter. While I project a 208 cutoff, there is plenty of room for error. We just aren’t able to correct for that error with percentiles.
Hello Mr. Sawyer. I achieved a PSAT score of 1450 and a selection index of 218. I live in Louisiana so I am pretty sure I made a high enough score for being a semifinalist but I am not sure about the “confirming” scores needed with the ACT and SAT. I got a 31 on the ACT this time around with 31M 34E 29R and I don’t know if that is a good enough score to confirm my PSAT scores. Should I be fine by using the ACT score I already have or should I prep to take it and/or the SAT again before the due date?
Thanks, Ethan
Ethan,
You have to use the ACT/SAT concordance tables to convert the ACT components to SAT scores and then calculate the SAT Selection Index. As you’ve already read, the Science score is not used. Your 31 Math is concordant with a 710 Math. Your 63 points (34+29) on English and Reading is concordant with a 690 ERW. This gives you an SAT SI of 69×2 + 71 = 209. The confirming level is usually set at the Commended cutoff, so that may be sufficient. I tend to be conservative, however, and would recommend retesting if you are intent on becoming a Finalist or Scholar. And your PSAT score indicates that you can probably do better. You can achieve a confirming score as late as December, so there is no rush.
Can you confirm that the ACT is still allowed as a confirming score for kids taking the NMSQT in fall of 2022 and graduating in 2024?
The change to allowing ACT was made several years ago and is permanent.
Thanks so much for this thorough explanation, Art. Do you know the rationale behind setting DC’s cutoff at the same number as the highest state’s? Does this mean that DC ends up with fewer semi-finalists than it deserves based on its percentage of high school graduates?
Michelle,
The rules NMSC uses for establishing cutoffs for selection units (non-state groups such as DC, students abroad, territories, boarding schools) are to ensure that these small groups don’t see cutoffs that are outside the norms. If DC were the 51st state, it would actually see fewer Semifinalists than it does now, and its cutoff would regularly be in the 224 range (maybe even 225). The same would be true for the relatively elite group of U.S. students studying abroad. On the other end, NMSC doesn’t allow the cutoff for any state or selection unit to fall below the Commended cutoff.
Hi, Art! I commented about a year ago asking for clarificationon something; yesterday, my National Merit application was finalized! Thanks for publishing such a helpful resource and answering everyone’s questions. Wish me luck!
You’re almost there! Best of luck in the next stages.
Hi Art,
A question about putting “Undecided” vs. first-choice college. My daughter is applying ED to her first-choice school and will likely find out in early December. She received a letter from that college today saying congrats on being a semifinalist and that if she designates them as her first-choice school and becomes a Scholar, she will get an automatic $X scholarship. She already turned in her application with “Undecided” … can she (or should she) go into her National Merit portal and try to change it to her ED school? What if she designates this school, but then gets deferred or denied?
Thank you,
Meredith
I would change her designation to her ED school. If she is denied, then she has plenty of time to change it. She just needs to remember to do it! Scholarship matching doesn’t happen until the spring. Things get a little more complicated if she is deferred. I would recommend keeping it as her first choice and then — should she be denied (let’s hope not) — change it immediately to the next NM school on her list.
Hi Art. I think my son has a great chance in KY for NMSF as Class of 2024 with a SI of 216. One quirky question. When the sub scores are doubled, shouldn’t all scores in theory be even numbers? Why are some semifinalist cutoffs odd numbers?
Kris,
The Math sub-scores can end in .5, so while the ERW component will always be even, the total Selection Index can be even or odd. A 215 might be a (35 + 35 + 37.5) x 2.
Hey! I was wondering if you think a 221 would be good for Texas this year? I know it’s kinda floating near the cutoff.
Ally,
You are in an excellent position. There is only the slimmest of slim chances that Texas would go up 2 points.
Thank you so much!
Dear Mr. Sawyer,
How do you feel about Virgina’s Thomas Jefferson School, which now refuses to notify students that they have received National Merit awards? See:
https://www.nationalreview.com/news/top-u-s-high-school-deprived-students-of-national-merit-awards-as-part-of-equity-policy/
Michael,
It seems like a misguided policy. It didn’t actually impact the award competition, but it did unnecessarily stress students who were expecting to be Commended.
Good evening. My son is a junior in Texas, and received an index score of 123 this past fall, so should be NMSF in the fall. But for a multitude of reasons, he is seriously considering doing a credit recovery program through his school district, and would possibly be able to graduate high school this June. He would then take a year off before applying to college. Would he still be able to be named a NMSF if he has already graduated? I didn’t think this scenario fit cleanly within the examples provided by NMSC on its website. Thank you!
Laura,
I’m assuming that you mean 223 for the Selection Index and not 123. Yes, he would be on a clear path to Semifinalist status. His early graduation should not impact that. National Merit allows students to take the PSAT in their last year of high school if they graduate early. To quote from National Merit:
“Those who take the PSAT/NMSQT in their last year of high school will be entering the competition for awards to be offered as they are completing their first year of college.”
This describes your son, except that he’ll be on gap year. If he continues to the Finalist stage, he’ll still need the support of his high school, even though he would have graduated.
Sorry, yes, 223. Thank you!
Hi would a selection index score of 205 in NY do anything? Does that have a “commended” status at least or is it nothing?
Laura,
205 is a good score on the PSAT. Unfortunately, it falls just below the Commended level.