SAT Subject Tests FAQ

Second semester of 11th grade is perhaps the most intense stretch of the college admission testing gauntlet that students must run. Many Compass students have just taken or are about to take their SAT or ACT, but for those applying to a highly selective college, there is no rest for the weary! It’s time to finalize a plan for Subject Tests targeting a test date of May and/or June. Subject Tests are expected by only about 20 of the most selective U.S. colleges and universities, but these institutions tend to attract the most attention from ambitious students.

• Choosing the subjects in which you have the most potential
• Nailing the timing of when you take the tests
• Ensuring that there are no gaps in your preparation

The best way to avoid tactical errors is to ensure each of these decisions is informed by the results of practice tests. We recommend taking an initial diagnostic test—one hour per subject—no later than 5 weeks before the official date you are considering. Our proctored test sessions and analysis of results are complimentary; however, advance reservations are required, and sessions close to popular test dates will fill up.

The good news is that an initial diagnostic test and review of the results may be all you need to do to be ready. Many students find that their academic coursework—particularly in AP and honors classes—is often sufficient as preparation for Subject Tests. And when additional tutoring for Subject Tests is needed, that prep tends to be both efficient and multi-purpose. Most students select Subject Tests that correspond with current academic classes, so tutoring for Subject Tests tends to serve double-duty as prep for an AP or final exam.

Subject Tests and Advanced Placement exams are often confused. Think of them as cousins, but not siblings. They serve different roles. Subject Tests are designed to allow students to demonstrate achievement in a particular academic area, but the tests are not tied to specific curricula and are expressly intended to be used in admission decisions. AP exams are more directly tied to a particular set of academic specifications. While APs certainly serve a role in admission decisions as evidence of mastery of the highest level offering of a particular subject, their original and official purpose is reflected in their moniker: “Advanced Placement.” Many colleges still link course placement and course credit to performance on AP exams. So while your AP classes will help inform your Subject Test planning, APs do not replace Subject Tests in the admission process (with very rare exceptions, e.g. NYU).

The answer depends entirely on the contours of the field on which a student intends to compete. While Subject Test scores are relevant at only about 3% of the four-year institutions in the U.S., the scores can be significant factors in the admission decisions at a little over 20 colleges that are extremely popular. And an additional 60 colleges—also quite well known—will consider Subject Tests if submitted.

To evaluate the tests’ importance in your individual situation, start by reviewing the list of these 100 institutions. If you’re an 11th grader, then you likely have a college list in mind to cross-reference. 10th graders usually aren’t as far along in their planning but may at least have an idea of whether the likes of Harvard, MIT, Princeton, Williams, etc. will be under consideration. You should also keep in mind that specific academic majors (e.g. engineering or nursing) within a college may require Subject Tests that are not required for all applicants to the college.

As a general rule, if you may decide to apply to one of the selective colleges in the up-to-date list on our website or to a particularly competitive academic major within a college, then you should keep your options open by taking Subject Tests.

The minimum expectation is two tests (with the sole exception of Georgetown, which still states a preference for three tests). Whether you should push yourself to exceed the minimum can be determined by a common sense assessment of the competitiveness of the applicant pool at your target colleges. Context is key.

For example: George Washington University and Stanford University will both consider Subject Tests. However, in 2014, GW admitted approximately 45% of the students who applied for admission, while Stanford admitted only 5%.

We would advise you to accept GW’s position at face value. You could reasonably conclude that while GW would like to see Subject Tests, it’s much more of a soft preference than an implied expectation.

On the other hand, and keeping in mind that a 5% admission rate made Stanford the most selective undergraduate institution in the country in 2014, it would be wise to exceed Stanford’s “will consider” by striving to produce outstanding Subject Test scores to submit if you possibly can.

A rule of thumb: The more competitive the applicant pool, the more you should interpret “recommended” as “expected” and “considered” as “recommended.” And if you could excel on more than the minimum of two Subject Tests without too much extra effort, then you should probably do so. It’s not uncommon for Compass’ most ambitious students to take three to five Subject Tests, if such an approach is supported by their academic coursework and strengths.

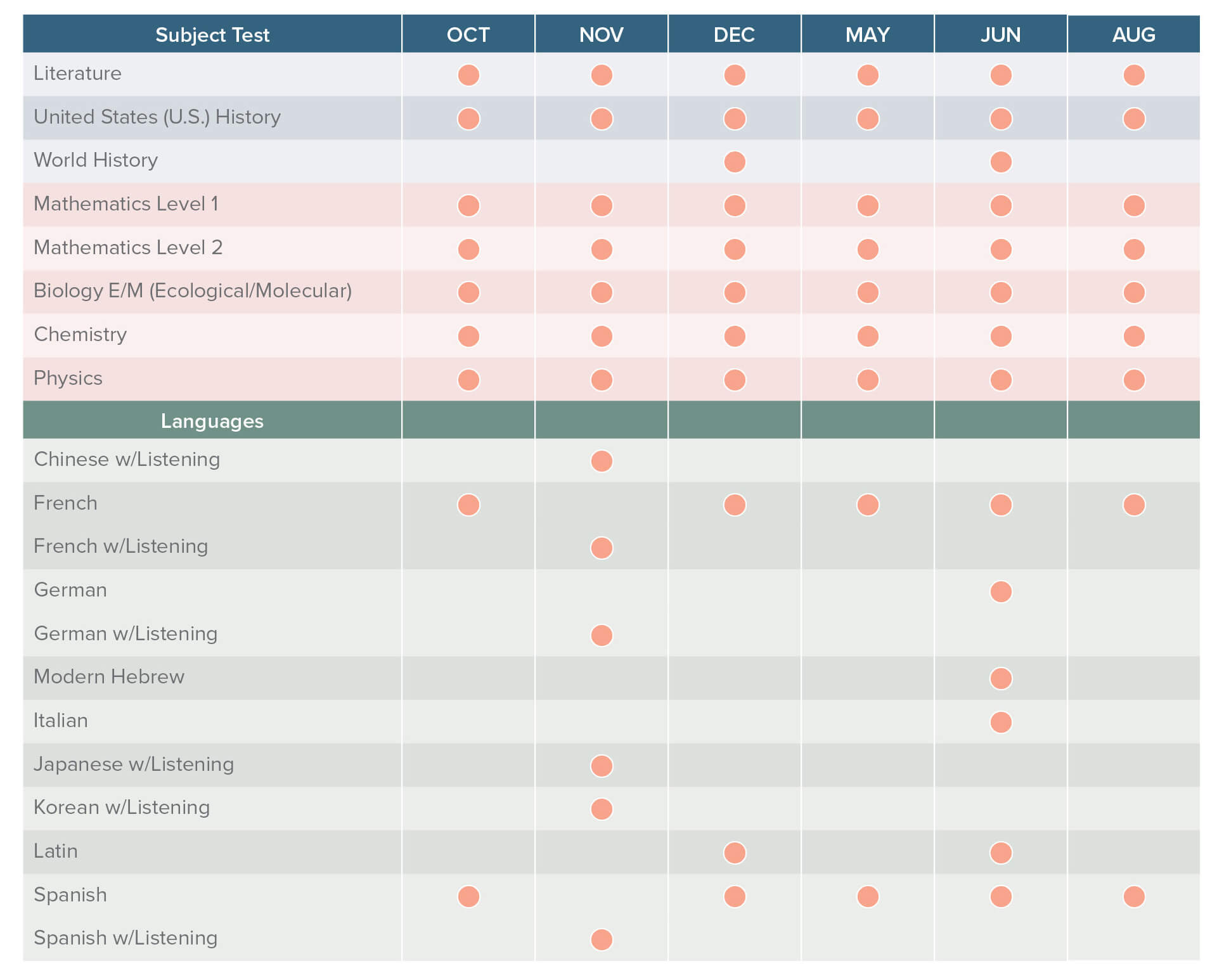
Optimal selection of Subject Tests is critical, and the best choices are usually those that align with your most advanced classes and your academic strengths. See the following list of subjects and months when each subject is offered, noting that not all subjects are offered on all test dates.

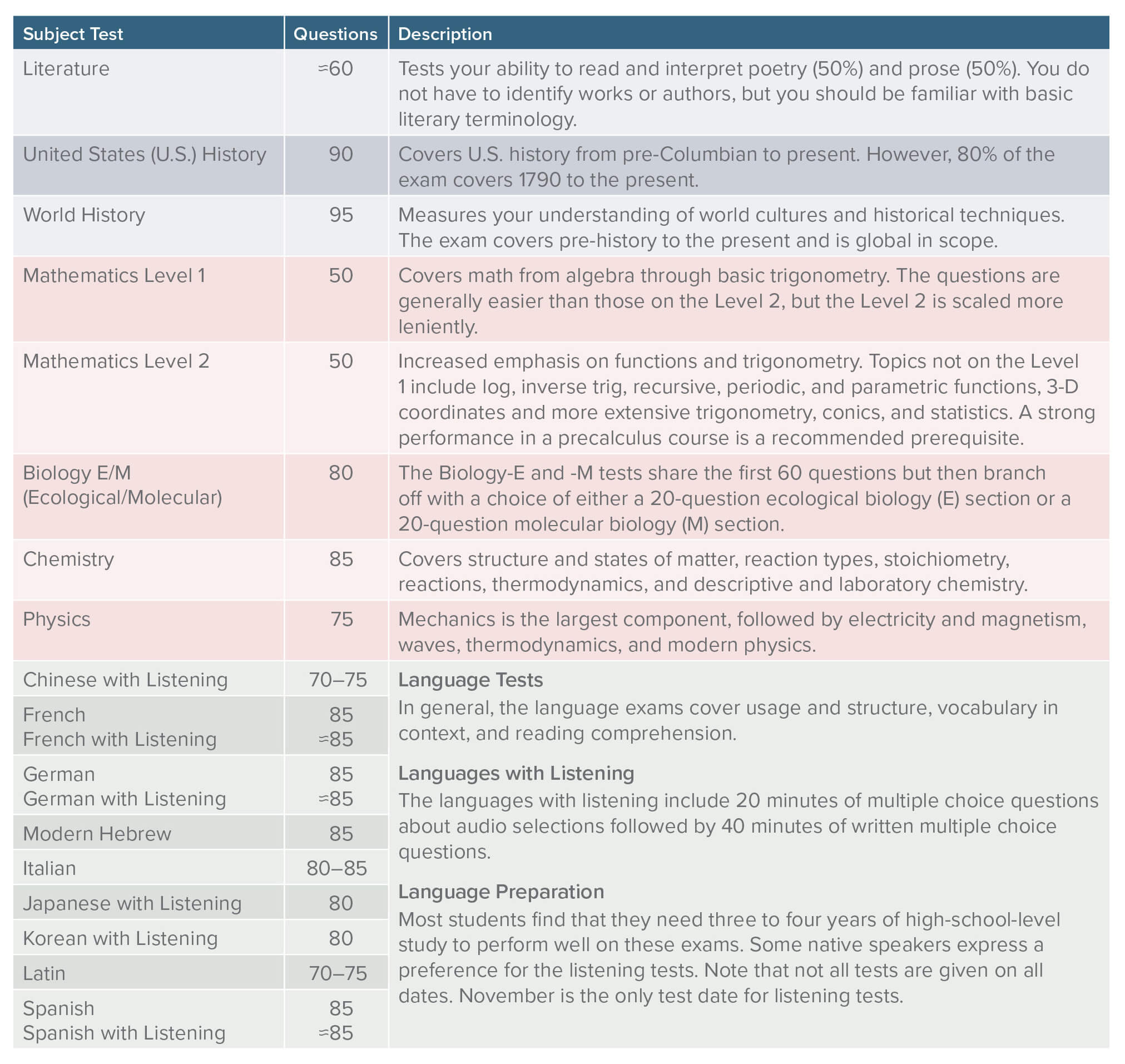
Here is a table detailing the number of questions and a brief description of each test:

Thoughts to keep in mind as you are evaluating these options relative to your classes at school and your academic strengths:

The more advanced and challenging the academic class, the more likely that the material will overlap significantly with a related Subject Test. If you are in an AP or honors/advanced class that corresponds with a Subject Test, then it is almost certainly advisable to at least take a practice test to evaluate whether you should take that Subject Test officially.

The alignment of content is not always straightforward though, and the practice test results must be interpreted with caution. Let’s take AP U.S. History for example:

A student expecting to score a 4 or 5 on AP-USH will find much content that is familiar on the ST-USH. However, we are not suggesting that even the top students in AP-USH should just walk into the ST-USH cold. The content overlap is not 100%. While most AP classes start with the arrival of the Europeans in the “New World,” the Subject Test takes the more enlightened view that Native American history is fair game too.

Then there is the rather fast pacing of Subject Tests. The ST-USH has 90-95 multiple-choice questions in just 60 minutes. Students must move quickly and act decisively. And decisiveness in the face of uncertainty is essential, as even the students most steeped in U.S. History may find a surprising number of questions with unfamiliar content. The test is designed to be approachable by students who have been taught U.S. History from a variety of pedagogical emphases. This broad but shallow characterization of the content means that very few high school history classes will have covered every stitch of material on the test, and therefore most students will need to make educated guesses or skip at least some questions. This also means that indecisive guessers and reluctant skippers may struggle to finish the exam.

Finally, the conversion scale reflects these realities of the test’s construction. A typical ST-USH scale allows students to leave as many as ten questions blank and still receive the top score of 800. Even students leaving half the questions blank could still score around 600.

With just a few exceptions, you should take a particular Subject Test at the end of the school year when you have taken a corresponding class of appropriate rigor. May or June of 11th grade is thus the most popular window when the majority of Subject Tests are taken. 10th and even 9th grade students may be advised to take a Subject Test, if they are excelling in an AP or advanced class in a subject that they will not continue in before 12th grade.

The choice between the May and June test dates requires careful consideration. June tends to be more popular, simply because it is later in the school year for most students and occurs very close to their final exams. It’s a lot to worry about simultaneously, but you get more bang (points) for your studying buck (time). Students in a corresponding AP class may find that their AP exam date is closer to the May date for Subject Tests than the June date. Would you rather study for the Subject Test first, knock that out, and then move on to the AP….or vice versa? We recommend you consult with your teacher at school. Many (but not all, unfortunately) teachers are well-versed in the Subject Test related to their specialty. They may be able to give subject-specific advice. Some may even tell you to take the AP first and wait until June for the Subject Test, because they plan to spend class time on the Subject Test material in the 1–3 week period between the AP date and the June date for Subject Tests.

Keep in mind that you can’t freely choose between May and June for Subject Tests if you have already planned to take the SAT on one of these test dates. You cannot take the SAT and the Subject Tests on the same date (we wouldn’t wish that on anybody even if it were possible). This is one of the reasons why we recommend a December, January, or March test date for a first sitting of the SAT. The ACT helpfully avoids College Board test dates, so the April and June ACT test dates do not pose a direct conflict. The June ACT date is always the second weekend in June, one week after the SAT / Subject Tests date. You could choose to utilize both of these June dates, in which case your summer break would be especially well earned.

The fall test dates are generally unpopular for Subject Tests. Thoughtful exceptions include an October tester who took an intensive summer school course or a November tester who wants to take the version of a Language test with a listening component (often preferred by native speakers). An unfortunate exception would be a student who somehow missed or failed to heed the advice to take Subject Tests at the end of the school year when students are most typically peaking in a particular subject.

Generally, yes. (See the next question for caveats related to colleges that disallow Score Choice.) The most typical retesting scenario would be to take a first stab on the May test date and then get right back on the horse for the June test date. Equestrian skills and test-taking skills tend to improve with experience, like most anything else. This May-then-June approach is a bit unusual though, as most students feel it will be sufficient to target just one test date and use practice tests (and possibly a modicum of tutoring) to ensure they are well prepared. Also, there is not time to test in May, wait to receive your score 2–3 weeks later, and then register for the June test date. The June registration deadline is earlier than the May score reporting date, so students wishing to keep the retest possibility open would need to pre-register for June well in advance. Those who sign up after the late registration deadline receive “Waitlist Status,” which does not guarantee a spot.

Another rationale for retesting would result from taking classes that build upon one another. For example, consider a 10th grader taking Honors Pre-Calculus. The content of the Math Level 2 aligns quite well with most Honors Pre-Calculus classes, so from that perspective the end of the 10th grade may be the optimal window. A 10th grader in this situation may be able to bank a top score on Math Level 2 and thus have less to worry about in 11th grade. Or, that 10th grader may find that there is still significant room for improvement after the first try, so he/she could decide to take another stab at it a year later. That student would typically go on to AP Calculus AB in 11th grade. The content of Calc AB is generally beyond the emphases of the Math Level 2, but math skills tend to be acquired cumulatively and retained. These further developed math skills specifically combined with another 12 months of academic maturity generally may be the ticket to an even higher Math 2 score.

If you’ve been paying attention at all, then you know what we rely on to help make these timing and retesting decisions. Practice tests! Never take an official test cold, and avoid speculation as much as possible in selecting tests and test dates.

Maybe. Technically the College Board gives you “Score Choice” capability, allowing you the ability to selectively report your scores as you see fit. You could, for example, take the Math 2, Literature, and Chemistry exams on the same test date and then later choose to report only certain scores from this date to any particular college. However, some colleges disallow Score Choice and require you to stipulate in your admission application that you have not exercised Score Choice. The “who” and “why” of this issue would require its own blog post, but try not to worry about it. If there is reason to believe that a retest would increase your score, then retest. If you retest and a particular college expects you to report both scores, then report both scores. The likelihood is extremely remote that any college would scrutinize the trend in your scores and discount a gain in any meaningful way.

If you find the variety of Score Choice postures confusing, here’s another head-scratcher: Many colleges require Subject Tests if paired with the SAT, but will officially accept the ACT alone as meeting the basic testing requirement. Let’s take two universities you may have heard of as examples: Harvard requires at least two Subject Tests IN ADDITION to EITHER the SAT or ACT, while Yale will fully consider your application for admission with ONLY an ACT score (Yale requires Subject Tests only if you chose to take the SAT instead of the ACT). Princeton and MIT are in Harvard’s camp on this issue, while Penn and Columbia see it Yale’s way. For a complete list, see the institutions listed in this table.

Confused yet? We don’t blame you. The pundits and gurus don’t all agree on why this variation in practices exists.

On the one hand, we are reluctant to suggest that any college’s policy should be taken at less than face value. If Yale’s policy says that an ACT alone is accepted equally in lieu of the SAT and several Subject Tests, who are we to suggest otherwise?

On the other hand, it’s possible that the option to submit an ACT score alone may make that college appear more welcoming to some prospective applicants, especially those in geographic locations or demographic circumstances in which Subject Tests are less readily available. For the typical Compass student in a competitive high school in California and carrying a schedule full of AP and Honors classes, we feel it is advisable to demonstrate academic strengths as convincingly as possible. In many cases this is best achieved by submitting Subject Tests regardless of whether they are technically required.

You can take as many as three Subject Tests on a test date, but you don’t have to take that many—you could take just one or two. You can choose to spread your Subject Tests across multiple test dates if your schedule allows. Each Subject Test is one hour long. Only having to cope with one or two Subject Tests on a certain date makes for a less taxing day, and this may reflect positively in your scores. It’s possible, for example, to take 1–2 Subject Tests in June of 10th grade, 1–2 more in May of 11th grade, and 1–2 more in June of 11th grade, with some of those tests serving as second attempts in the same subject. Each student has unique circumstances and strengths, so there is no static template.

Up to the very last minute. While the registration form for Subject Tests asks you to indicate which subjects you intend to take (we’re not sure why), this is non-binding. On the day of the test, you are given a thick booklet with all subjects, and you choose then and there which subjects you will take. Don’t worry: If you decide to take more subjects than you paid for when you registered, the College Board will remember to bill you for the difference.

Yes, you choose the order. Most students choose to start with the subject on which they feel they need the most energy and/or are most hopeful will be their best subject, but this is entirely up to you.

We’re sorry to keep saying “It depends,” but, well….it really does depend on the context. While few institutions readily report Subject Test data for admitted or enrolled students, we can make some reasonable assumptions. SAT score data in the middle-50th percentiles (25th % to 75th %) are available, and it stands to reason that Subject Test scores for enrolled students are similar to SAT scores. Students can expect that Subject Test scores in the low-mid 700s put them in the same ballpark as other applicants to the highly selective colleges that require Subject Tests.

When evaluating your Subject Test scores, focus on the scaled score from 200–800 and not the reported percentile. Percentile scores for Subject Tests are misleading, because they often indicate a skewed testing population. For example, only 27,000 students take the Physics test each year, so it is logical to assume that most are quite good at Physics. Your scaled score, not your percentile, is the most important number on your Subject Test report and allows you to compare your performance across different subjects.